背景
GBDT(gradient boosting decision tree)是机器学习中的一类经典算法,也是kaggle, 天池这些机器学习比赛中常见的解决方案。在chatGPT发布后带来的all in神经网络的背景下,GBDT依旧凭借其较好的解释性、不错的性能、较低的训练成本以及更加容易上手的学习曲线,值得想要参与机器学习比赛的新手玩家去学习。本文主要总结一下GBDT算法的基本理论。
决策树模型与集成学习
这里不再赘述决策树模型的基本原理,只需将决策树视为如下数学模型
\[f(x) = \sum_{m=1}^{n}w_{m}I_{\{x\in R_{m}\}}\]其中$x$是样本数据,$x\in R^{d}$,$n$为决策树的叶节点数目,$I_{{x\in R_{m}}}$为指示函数,$x$落在$R^{d}$中的区域$R_{m}$时为1,否则为0,区域$R_{m}$两两不交,$w_{m}\in R$。
对回归树,需要确定划分$R_{m}$和权重$w_{m}$,使得$loss(y_{true},f(x))$最小。对二分类,我们只需将输出的$f(x)$通过logit函数转化为概率值,即
\[logit(x) = \frac{1}{1+\exp(-f(x))}\]对多分类任务,利用”one vs all”准则可将其分解为多个二分类任务。因此我们仅讨论回归树情形。
对集成学习,简单讲就是使用多个弱学习器去训练一个强学习器的结果。例如可以训练多颗决策树,每棵树预测取平均作为最终输出。这种做法直觉上看是保证了结果的鲁棒性。假设每棵树的训练误差$e_{i}$独立同分布,有
\[E[e] = \mu, Var(e) = \sigma^{2}\]当我们将结果取均值时,我们有
\[E[\frac{1}{n}\sum_{i=1}^{n}e_{i}] =\frac{1}{n}\sum_{i=1}^{n}E[e_{i}] = \mu\] \[Var(\frac{1}{n}\sum_{i=1}^{n}e_{i}) = \frac{1}{n^{2}}\sum_{i=1}^{n}Var(e_{i}) = \frac{1}{n}\sigma^{2}\]可以看到这种简单的均值集成是控制了预测误差的方差,并没有减少误差期望$\mu$。
为了减小$\mu$,通常考虑Boosting算法,Boosting常见的有两种,一种是Adaboost,根据先前训练的结果去调整样本权重,另一种则是Gradient Boosting,根据先前训练的误差去训练一颗新的树拟合误差。下面我们主要讨论Gradient Boosting的思想。
Gradient Boosting
Gradient Boosting 可以类比最优化算法中的梯度下降方法。假设前$m$步得到的模型为
\[F_{m}(x) = \sum_{i=1}^{m}f_{i}(x)\]这里的$f_{i}$代表第$i$步训练得到的决策树,记第$m$步的预测值为$y_{m}$,真实值为$y$,有训练损失$loss(y_{m},y)$。
现在考虑加入$f_{m+1}(x)$,同时减小$loss(y_{m}+f_{m+1}(x),y)$,可以看到,当$f_{m+1}(x) = -\eta \frac{\partial loss}{\partial \hat{y}} \vert_{\hat{y} = y_{m}}$时,其中 $\eta$ 为足够小的正数,此时一定有
\[loss(y_{m}+f_{m+1}(x),y) \leq loss(y_{m},y)\]因此,在训练下一棵决策树时,其拟合的目标值应当为$-\eta \frac{\partial loss}{\partial \hat{y}}\vert_{\hat{y} = y_{m}}$,这也是算法名字中Gradient的由来。
GBDT三件套
下面要介绍的是GBDT方法中最流行的三个模型,分别是XGBoost(xgb), LightGBM(lgb)和CatBoost(cat)。
三个模型的特点,xgb是在先前的gradient boosting的基础上,引入了二阶梯度提高精度,二阶梯度在lgb,cat中应该也都有用到,lgb,cat的自定义目标函数中都要求输入一阶梯度和二阶梯度的信息。lgb的主要特点就是轻量化(Light),个人感觉是比xgb要快的,另外就是加入了梯度采样和特征捆绑的设计。cat主要强调的是类别特征。
一般来讲,三种方法性能基本一致,不同的数据集上会略有差异,因此建议三种方法都试一下,选择效果最好的或者是集成一下。应用层面上,三种方法的API比较相似,掌握一个之后就能很快上手其他两个。下面介绍一下二阶梯度的思想。
gradient boosting 考虑$min \; loss(y_{m}+f,y)$, 对$loss$项做关于$\hat y$做泰勒展开至二阶,有
\[\small \begin{equation} loss(y_{m} + \eta f,y) = loss(y_{m},y) +\eta \frac{\partial loss}{\partial \hat{y}}|_{\hat y = y_{m}} f +\eta^{2} \frac{1}{2}\frac{\partial^{2} loss}{\partial \hat{y}^{2}}\vert_{\hat y = y_{m}} f^{2} + o(\eta^2 f^2) \end{equation}\]当$\eta$足够小时,
\[\small loss(y_m + \eta f,y) \sim loss(y_{m},y) +\eta \frac{\partial loss}{\partial \hat{y}}|_{\hat y = y_{m}} f +\eta^{2} \frac{1}{2}\frac{\partial^{2} loss}{\partial \hat{y}^{2}}\vert_{\hat y = y_{m}} f^{2}\]这时可以通过最小化这个二阶泰勒展开,得到新的$f$,使得 \(loss(y_{m}+f,y) \leq loss(y_{m},y)\) 直觉上看,由于二阶泰勒展开的误差项是二阶的,因此当训练误差较小时,理论上能够实现比GBDT更小的误差。
xgboost的具体实现
参考陈天奇的论文1,有
\[\begin{align} L^{t} &= \sum_{i=1}^{n}[g_i f_{t}(x_{i}) + \frac{1}{2}h_{i}f_{t}^{2}(x_i)] + \Omega(f_t) \\ & = \sum_{i=1}^{n}[g_i f_{t}(x_{i}) + \frac{1}{2}h_{i}f_{t}^{2}(x_i)] + \gamma T + \frac{1}{2}\lambda \sum_{j=1}^{T}\omega_{j}^2 \\ &= \sum_{j=1}^{T}[(\sum_{i\in I_{j}}g_i)\omega_j + \frac{1}{2}(\sum_{i\in I_{j}}h_i+\lambda)w_{j}^{2}] + \gamma T \end{align}\]这里$g_i, h_i$是第$i$个样本的损失的一阶和二阶梯度,$\Omega(f)$是正则项,$I_j$是第$j$个叶节点(样本空间划分)下的样本集合,$T$是叶节点的数量。
在给定划分$I_j$的情况下,可以显示的算出最优的$w_j = -\frac{\sum_{i\in I_j}g_i}{\sum_{i\in I_j}h_i + \lambda}$,对应$L^{t}$的最优值为$-\frac{1}{2}\sum_{j=1}^{T}\frac{(\sum_{i\in I_j}g_i)^2}{\sum_{i\in I_j}h_i+\lambda} + \gamma T$。这个数值也可以用来评估一个划分的好坏。
在实际情形中,遍历所有划分是不可能的,对 $n$ 个样本,即使是一个特征,其所有可能划分有$2^{n}$。因此实际应用中仅考虑二叉树的情形,即根据一个特征将样本划分为$I_{L} = {i \vert x_{i} \leq \alpha}$,$I_{R} = {i \vert x_{i} > \alpha}$,这样仅需考虑 $n$ 个划分。此时划分前后,loss变化如下:
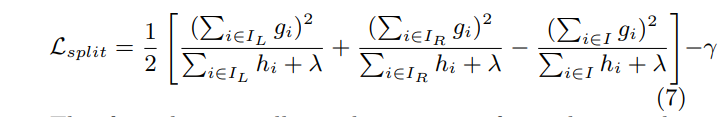
根据上述公式去选择最优的划分$I_{L},I_{R}$。
关于xgboost的思考
-
如果不是二叉树结构,每个节点划分的复杂度(需要考察的划分次数)会是多少?
假设为$d$叉树,复杂度应该为$C_{n}^{d-1}$。因此在样本很大的情形下,多叉的划分的复杂度会非常高。
-
二阶梯度的作用?
前面的推导中,利用二阶泰勒展开将原本的损失函数使用二次函数完成逼近,因此节点划分与叶节点权重确认转化为一个最小化二次函数的问题。当二次函数非正定的情形下,最小值为$-\infty$,决策输的训练 ill-conditioned。例如在MAE损失的情形下,二阶导数为0,此时若使用custom objective并定义二阶导数为0,训练是无法进行的。下面展示了一些不同的custom objective在lgb下的实验结果,来说明gbdt算法中必须选择正定的二次函数来逼近。
下面的这组实验尝试了如下custom objective,首先尝试了一个错误定义的二次损失函数$||y-\hat{y}||^{2}$,错误的定义二阶梯度 tmp_2 为0,发现训练无法进行,之后正确的定义二阶梯度为 np.ones ,误差能够减小,最后再次尝试一个错误的负二阶梯度-np.ones, 训练再次无法进行。
### 数据来自于2023年阿里天池云AI4bio比赛 from sklearn.model_selection import train_test_split train_data,val_data,age_train, age_val, health_train,health_val = train_test_split(train, age,health, test_size = 0.2, stratify=health) def wrong_o2(y_pred,train_data): y_true = train_data.get_label() tmp_1 = y_pred - y_true tmp_2 = np.zeros(tmp_1.shape[0]) return tmp_1,tmp_2 obj = wrong_o2 lgb_train = lgb.Dataset(train_data,label=age_train) lgb_val = lgb.Dataset(val_data,age_val,reference=lgb_train) params = {'learning_rate': 0.1, 'reg_lambda': 0, 'reg_alpha': 0, 'seed': 33, 'verbose':-1, 'objective':obj, 'metric':'mae'} gbm = lgb.train(params, lgb_train, valid_sets = [lgb_train,lgb_val], fobj=obj, callbacks=[lgb.log_evaluation(10)], num_boost_round=100) ### Output [10] training's l1: 53.6583 valid_1's l1: 53.6654 [20] training's l1: 53.6583 valid_1's l1: 53.6654 [30] training's l1: 53.6583 valid_1's l1: 53.6654 [40] training's l1: 53.6583 valid_1's l1: 53.6654 [50] training's l1: 53.6583 valid_1's l1: 53.6654 [60] training's l1: 53.6583 valid_1's l1: 53.6654 [70] training's l1: 53.6583 valid_1's l1: 53.6654 [80] training's l1: 53.6583 valid_1's l1: 53.6654 [90] training's l1: 53.6583 valid_1's l1: 53.6654 [100] training's l1: 53.6583 valid_1's l1: 53.6654 def true_o2(y_pred,train_data): y_true = train_data.get_label() tmp_1 = y_pred - y_true tmp_2 = np.ones(tmp_1.shape[0]) return tmp_1,tmp_2 obj = true_o2 lgb_train = lgb.Dataset(train_data,label=age_train) lgb_val = lgb.Dataset(val_data,age_val,reference=lgb_train) params = {'learning_rate': 0.1, 'reg_lambda': 0, 'reg_alpha': 0, 'seed': 33, 'verbose':-1, 'metric':'mae'} gbm = lgb.train(params, lgb_train, fobj = obj, valid_sets = [lgb_train,lgb_val], callbacks=[lgb.log_evaluation(10)], num_boost_round=100) ### Output [10] training's l1: 23.0765 valid_1's l1: 23.4346 [20] training's l1: 16.1578 valid_1's l1: 17.0966 [30] training's l1: 13.879 valid_1's l1: 15.4632 [40] training's l1: 12.6867 valid_1's l1: 14.7725 [50] training's l1: 11.8599 valid_1's l1: 14.3585 [60] training's l1: 11.2243 valid_1's l1: 14.0723 [70] training's l1: 10.6601 valid_1's l1: 13.7895 [80] training's l1: 10.1667 valid_1's l1: 13.5953 [90] training's l1: 9.72681 valid_1's l1: 13.4159 [100] training's l1: 9.31697 valid_1's l1: 13.2625 def wrong_o2(y_pred,train_data): y_true = train_data.get_label() tmp_1 = y_pred - y_true tmp_2 = np.ones(tmp_1.shape[0]) return tmp_1,-tmp_2 obj = wrong_o2 lgb_train = lgb.Dataset(train_data,label=age_train) lgb_val = lgb.Dataset(val_data,age_val,reference=lgb_train) params = {'learning_rate': 0.1, 'reg_lambda': 0, 'reg_alpha': 0, 'seed': 33, 'verbose':-1, 'metric':'mae'} gbm = lgb.train(params, lgb_train, fobj = obj, valid_sets = [lgb_train,lgb_val], callbacks=[lgb.log_evaluation(10)], num_boost_round=100) ### Output [10] training's l1: 53.6583 valid_1's l1: 53.6654 [20] training's l1: 53.6583 valid_1's l1: 53.6654 [30] training's l1: 53.6583 valid_1's l1: 53.6654 [40] training's l1: 53.6583 valid_1's l1: 53.6654 [50] training's l1: 53.6583 valid_1's l1: 53.6654 [60] training's l1: 53.6583 valid_1's l1: 53.6654 [70] training's l1: 53.6583 valid_1's l1: 53.6654 [80] training's l1: 53.6583 valid_1's l1: 53.6654 [90] training's l1: 53.6583 valid_1's l1: 53.6654 [100] training's l1: 53.6583 valid_1's l1: 53.6654上述尝试中,我们是故意定义了两个错误的梯度,发现 lgb 无法正常训练。训练无法进行到底是由于损失函数求导错误还是二次导数小于等于零导致的无法确定,因此下面尝试正确定义导数但是非正定的目标函数。定义损失函数为$||y - \hat{y}||^{3}$,目标函数的二阶梯度符号不定,结果发现无法正常训练。
def o3(y_pred,train_data): y_true = train_data.get_label() tmp_1 = 3*np.power(y_pred - y_true,2) tmp_2 = 6*(y_pred - y_true) return tmp_1,tmp_2 obj = o3 lgb_train = lgb.Dataset(train_data,label=age_train) lgb_val = lgb.Dataset(val_data,age_val,reference=lgb_train) params = {'learning_rate': 0.1, 'reg_lambda': 0, 'reg_alpha': 0, 'seed': 33, 'verbose':-1, 'metric':'mae'} gbm = lgb.train(params, lgb_train, fobj = obj, valid_sets = [lgb_train,lgb_val], callbacks=[lgb.log_evaluation(10)], num_boost_round=100) ## output [10] training's l1: 53.6583 valid_1's l1: 53.6654 [20] training's l1: 53.6583 valid_1's l1: 53.6654 [30] training's l1: 53.6583 valid_1's l1: 53.6654 [40] training's l1: 53.6583 valid_1's l1: 53.6654 [50] training's l1: 53.6583 valid_1's l1: 53.6654 [60] training's l1: 53.6583 valid_1's l1: 53.6654 [70] training's l1: 53.6583 valid_1's l1: 53.6654 [80] training's l1: 53.6583 valid_1's l1: 53.6654 [90] training's l1: 53.6583 valid_1's l1: 53.6654 [100] training's l1: 53.6583 valid_1's l1: 53.6654小结
以上是个人学习xgb,lgb,cat中的一些思考与总结,了解其基本原理有助于根据训练表现针对性的调参。同时,泰勒展开二阶逼近是这些算法较先前gbdt性能提升的一个重要原因,在自定义训练损失时要特别注意二阶梯度项。后面将结合具体的任务展示这些算法的使用方法。
参考文献
- [1] Chen, Tianqi, and Carlos Guestrin. “Xgboost: A scalable tree boosting system.” Proceedings of the 22nd acm sigkdd international conference on knowledge discovery and data mining. 2016.