变分推断总结

最近做单细胞多组学数据整合分析时，用到了MOFA¹这个基于变分推断的多组学整合方法，于是决定花点时间学习一下变分推断这部分内容，这篇博客是自己学习变分推断过程中的一点笔记。阅读这篇笔记需要对参数推断、最优化内容有一定的了解。

变分推断(variational inference)

在贝叶斯统计中，一个常见的问题是后验概率的推断，记$x$是观测值，$z$是隐变量，希望得到$p(z\vert x)$。由贝叶斯公式，我们有

\[\begin{equation} p(z \vert x) = \frac{p(z,x)}{p(x)} = \frac{p(z,x)}{\int p(z,x) \mathop{}\mathrm{d}z} \end{equation}\]

但在实际计算中，$\int p(z,x) \mathop{}\mathrm{d}z$ 通常是难以显示计算的，因此考虑其他的策略来估计$p(z \vert x)$。

考虑如下优化问题

\[\begin{equation} \min_{q \in \mathcal{L}} \mathrm{KL}(q(z) \vert \vert p(z \vert x)) = \mathrm{E}_{q} \log (q(z) \vert \vert p(z \vert x)) \end{equation}\]

将问题转化为在一个特定分布族中，寻找与$p(z \vert x)$最接近的概率分布的变分问题。考虑一类特殊的分布族，平均场变分分布族(mean-field variational family)

\[\begin{equation} q(z) = \prod_{j=1}^{J}q_{j}(z_{j}) \end{equation}\]

即隐变量的各个分量独立。上述假设使得我们可以通过逐次坐标优化的策略去求解优化问题的一个局部最优值。

定义$z_{j}$的完全条件概率为给定观测$x$和$z$中除$z_{j}$之外的所有分量的条件概率，记为$p(z_{j} \vert z_{-j},x)$。那么利用变分中的欧拉-拉格朗日方程，能够得到$q_{j}^{*}(z_{j})$的最优解为

\[\begin{equation} q_{j}^{*}(z_{j} ) \propto \exp \{\mathrm{E}_{-j} [ \log p(z_{j} \vert z_{-j},x)]\} \end{equation}\]

其中$\mathrm{E_{-j}}$是相对于概率密度$\prod_{i\neq j}q(z_{i})$的期望，该结果具体计算过程如下:首先处理$KL$散度，

\[\begin{equation} \begin{aligned} \mathrm{KL}(q(z) \vert \vert p(z \vert x)) &= \mathrm{E}_{q}[\log q(z) - \mathrm{\log p(z \vert x)}] \\ &= \mathrm{E}[\log q(z) - \mathrm{\log p(z,x)}] + \log p(x) \\ &= - \mathrm{ELBO(q(z))} + \log p(x) \end{aligned} \end{equation}\]

其中$\mathrm{ELBO}(q)$被称作evidence lower bound，在变分推断中，最小化$\mathrm{KL}$散度常被转化为最大化$\mathrm{ELBO}$。在平均场假设下，我们有

\[\begin{equation} \mathrm{ELBO}(q) = \int [\log p(z,x) - \sum_{j} \log q(z_{j})](\prod_{j}q(z_{j})) \mathop{} \mathrm{d} z \end{equation}\]

变分法中的欧拉-拉格朗日方程告诉我们，对一个关于函数$y$的泛函$J(y) = \int F(x,y,y_{x}) \mathop{} \mathrm{d} z$, $J(y)$取极值时$y(x)$满足如下条件：

\[\begin{equation} \frac{\partial F}{\partial y} - \frac{\mathrm{d}}{\mathrm{d}x}(\frac{\partial F}{\partial y_{x}} ) = 0 \end{equation}\]

仅考虑$z_{j}$的情况下，我们有

\[\begin{equation} \scriptsize \begin{aligned} \mathrm{ELBO}(q(z_{j})) &= \int [\int [\log p(z_{j},z_{-j},x) - \log q(z_{j}) - \sum_{i\neq j}\log q(z_{i}) ]q(z_{j}) \mathop{} \mathrm{d}z_{j}] \prod_{i \neq j} q(z_{i}) \mathop{} \mathrm{d}z_{-j} \\ \frac{\partial \mathrm{ELBO(q(z_{j}))}}{\partial q(z_{j})} &= \int [\log p(z_{j},z_{-j},x) - \log q(z_{j}) - \sum_{i\neq j}\log q(z_{i}) - \frac{1}{q(z_{j})}q(z_{j})]\prod_{i \neq j} q(z_{i}) \mathop{} \mathrm{d}z_{-j} \\ & = \int [\log p(z_{j},z_{-j},x) - \log q(z_{j})]\prod_{i \neq j} q(z_{i}) \mathop{} \mathrm{d}z_{-j} + C \\ & = \int [\log p(z_{j},z_{-j},x)]\prod_{i \neq j} q(z_{i}) \mathop{} \mathrm{d}z_{-j} - \log q(z_{j})+ C \\ & = \mathrm{E}_{-j} [ \log p(z_{j},z_{-j},x)] - \log q(z_{j}) + C = 0 \end{aligned} \end{equation}\]

至此完成$q_{j}^{*}(z_{j})$的计算。相应的变分推断算法如下：

图一：CAVI算法

随机变分推断(stochastic variational inference)

模型假设

变分推断的一个问题在于难以处理大规模数据，由于其使用的坐标上升算法，在隐变量规模很大的情形下，更新隐变量参数的计算开销很大。随机变分推断的提出很好的解决了这个问题。

考虑如下所示的概率图模型，

图二：随机变分推断概率图模型

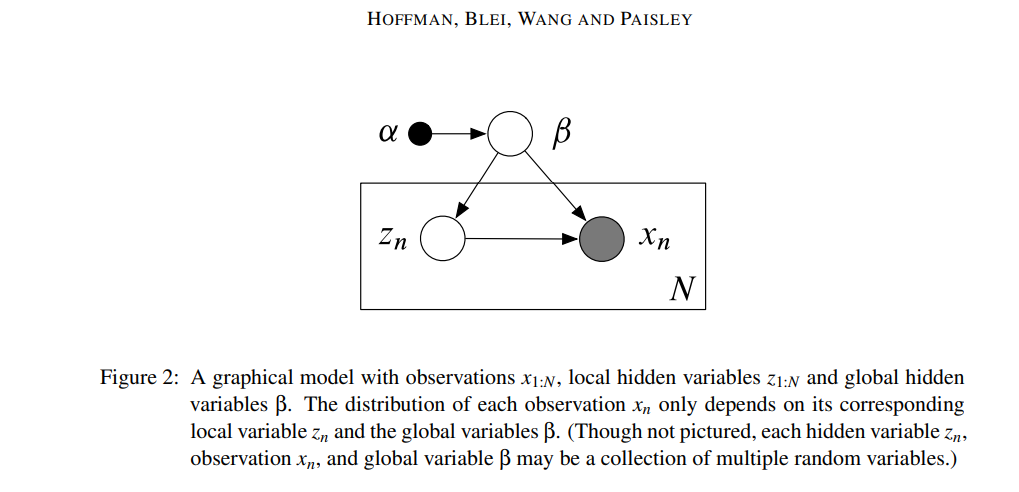
在上述模型中，有N个观测值$x_{n}$,每个观测值有一个local的隐变量$z_{n} = (z_{n,1},z_{n,2},…,z_{n,J})$，对所有观测值存在一个global隐变量$\beta$以及global参数$\alpha$。随机变分推断的模型假设如下:

\[\begin{align} p(x_{n},z_{n} \vert x_{-n},z_{-n},\beta,\alpha) &= p(x_{n},z_{n} \vert \beta,\alpha) \tag{9-0}\\ p(x,z,\beta \vert \alpha) &= p(\beta \vert \alpha) \prod_{n=1}^{N}p(x_{n},z_{n} \vert \beta) \tag{9-1} \\ p(\beta \vert x,z,\alpha) &= h(\beta)\exp(\eta_{g}(x,z,\alpha)^{t}t(\beta) - a_{g}(\eta_{g}(x,z,\alpha))) \tag{9-2} \\ p(z_{n,j} \vert x_{n},z_{n,-j},\beta) &= h(z_{n,j}) \exp (\eta_{l}(x_{n},z_{n,-j},\beta)t(z_{n,j}) - a_{l}(\eta_{l}(x_{n},z_{n,-j},\beta))) \tag{9-3} \\ p(x_{n},z_{n} \vert \beta) &= h(x_{n},z_{n})\exp(\beta^{t}t(x_{n},z_{n}) - a_{l}(\beta)) \tag{9-4} \\ p(\beta) &= h(\beta) \exp(\alpha^{t} t(\beta) - a_{g}(\alpha)) \tag{9-5} \end{align}\]

其中,假设(9-0)说明了在给定全局隐变量$\beta$的情形下，局部数据$(x_{n},z_{n})$和其他数据是条件独立的。假设(9-1)是图二对应的概率图模型的联合概率密度，假设(9-2,9-3)声明了完全条件概率是指数族分布，假设(9-4,9-5)声明了先验概率是指数族分布。进一步假设$(x_{n},z_{n})和\beta$是共轭概率分布，计算可得假设(9-5)中的充分统计量$t(\beta) = (\beta, -a_{l}(\beta))$，对应的$\alpha = (\alpha_{1},\alpha_{2})$,假设(9-2)中的$\eta_{g}(x,z,\alpha) = (\alpha_{1} + \sum_{n=1}^{N}t(x_{n},z_{n}),\alpha_{2} + N)$。

考虑平均场假设，并且假设平均场下的概率分布和先验概率形式一致，有

\[\begin{align} q(z,\beta) &= q(\beta \vert \lambda)\prod_{n=1}^{J}\prod_{j=1}^{J}q(z_{nj} \vert \phi_{nj}) \tag{9-6} \\ q(\beta \vert \lambda) &= h(\beta) \exp(\lambda^{t}t(\beta) - a_{g}(\lambda)) \tag{9-7} \\ q(z_{nj} \vert \phi_{nj}) &= h(z_{nj}) \exp(\phi_{nj}^{t}t(z_{nj}) - a_{l}(\phi_{nj})) \tag{9-8} \end{align}\]

变分推断求解

现在仅考虑$\lambda$的估计，记$\mathrm{ELBO}(q) = L(q)$,有

\[%\begin{equation} \begin{align} L(\lambda) &= E_{q}[\log p(x,z,\beta)] - E_{q}[\log q(\beta,z) ] \\ & = E_{q}[\log p(\beta \vert x,z)] - E_{q}[\log q(\beta)] + C \tag{9-9} \end{align} %\end{equation}\]

代入(9-2,9-6,9-7)计算，有

\[\small %\begin{equation} \begin{align} L(\lambda) &= E_q[\log h(\beta) + \eta_{g}(x,z,\alpha)^{t} t(\beta) - a_{g}(\eta_{g}(x,z,\alpha))] - E_{q}[\log h(\beta) + \lambda^{t} t(\beta) - a_{g}(\lambda)] \\ &= E_q[\eta_{g}(x,z,\alpha)]^{t}E_{q}[t(\beta)] - a_{g}(\eta_{g}(x,z,\alpha)) -\lambda^{t}E_{q}[t(\beta)] - a_{g}(\lambda) \\ &= E_q[\eta_{g}(x,z,\alpha)]^{t} \nabla_{\lambda}a_{g}(\lambda) -\lambda^{t}\nabla_{\lambda}a_{g}(\lambda)- a_{g}(\lambda) + C \tag{9-10} \end{align} %\end{equation}\]

这里用到指数分布族的性质，充分统计量的期望$E_{q}[t(\beta)] = \nabla_{\lambda}a_{g}(\lambda)$，该性质的推导见网页²。

由

\[\nabla_{\lambda} L(\lambda) = \nabla^{2}_{\lambda} a_{g}(\lambda) (E_{q}[\eta_{g}(x,z,\alpha)] - \lambda) = 0\]

得到全局变量$\lambda$的更新

\[\lambda = E_{q}[\eta_{g}(x,z,\alpha)]\]

类似的可以计算

\[\phi_{nj} = E_{q}[\eta_{l}(x_n,z_{n,-j},\beta)]\]

以上参数的更新也可以由(4)得到，

\[\begin{aligned} q(\beta \vert \lambda) &\propto \exp \{E_{-\beta}[\log p(\beta \vert x,z,\alpha)]\} \\ &= \exp \{E_{-\beta}[\log h(\beta) + \eta_{g}(x,z,\alpha)^{t}t(\beta) - a_{g}(\eta_{g}(x,z,\alpha))]\} \\ &=h(\beta)\exp\{E_{-\beta}[\eta_{h}(x,z,\alpha)]^{t}t(\beta) - C\} \end{aligned}\]

图三：变分推断算法

上述算法存在一个问题，在更新全局参数$\lambda$前，需要更新全部的局部参数$\phi$。由于初始时$\lambda$是随机设置的，因此可能开始时会在一个较差的全局参数估计的基础上进行大量局部参数的更新。一个提升效率的想法是，可以根据部分数据去更新全局参数，这样可以避免在算法起步的阶段浪费大量的时间。

随机变分推断求解

图三中的算法是从逐坐标优化的角度给出的，现在从梯度上升的角度去考虑。对于$L(\lambda)$,先前我们计算得到梯度如下

\[\nabla_{\lambda} L(\lambda) = \nabla^{2}_{\lambda} a_{g}(\lambda) (E_{q}[\eta_{g}(x,z,\alpha)] - \lambda)\]

对光滑函数来讲，在足够小的步长$\rho >0$下，有$f(x + \rho \nabla f(x))\geq f(x)$,因此有更新

\[\lambda_{t+1} = \lambda_{t} + \rho\nabla^{2}_{\lambda} a_{g}(\lambda_t) (E_{q}[\eta_{g}(x,z,\alpha)] - \lambda_t)\]

因此，上一节中$\lambda$的更新也可以看做是步长

\[\rho={\nabla^{2}_{\lambda} a_{g}(\lambda_t)}^{-1}\]

的梯度下降。

对变分参数直接进行梯度下降面临一个问题，梯度下降是在变分参数的欧式空间下进行的，但是两个变分参数差异很小的分布不一定在概率分布空间中接近。例如$\mathcal{N}(0,0.01)$和$\mathcal{N}(0.1,0.01)$在概率空间中差异很大，但在变分参数空间中差异很小。为解决这一问题，需要在新的度量下去计算梯度，因此引入natural gradient的概念。关于这部分的讨论，见参考文献³。这里我们只要知道在优化变分参数时，使用如下的natural gradient是更好的选择

\[\begin{aligned} \hat{\nabla}_{\lambda} L &= E_{q}[\eta_{g}(x,z,\alpha)] - \lambda \\ \hat{\nabla}_{\phi_{n,j}} L &= E_{q}[\eta_{l}(x_{n},z_{n,-j},\alpha)] - \phi_{n,j} \end{aligned}\]

只考虑对$\lambda$的更新，注意到

\[\begin{equation} \begin{aligned} L(\lambda) &= E_{q}[\log p(x,z,\beta)] - E_{q}[\log q(\beta,z) ] \\ & = E_{q}[\log p(x,z \vert \beta)] + E_q[\log p(\beta)]- E_{q}[\log q(\beta)] - E_q [\log q(z)] \\ & = \underbrace{E_{q}[\log p(\beta)] - E_q [\log q(\beta)]}_{global\; term} + \underbrace{\sum_{i=1}^{N}E_{q}[\log p(x_n,z_n \vert \beta) - \log q(z_n)]}_{local \; term} \end{aligned} \end{equation}\]

对于local term的无偏估计，可以通过从$x_{1},…x_{N}$中抽样实现。定义

\[L_I(\lambda) =E_{q}[\log p(\beta)] - E_q [\log q(\beta)] + NE_{q}[\log p(x_I,z_I \vert \beta) - \log q(z_I)]\]

其中$I$是${1,2,…N}$中的均匀随机变量，可以基于$L_{I}(\lambda)$得到natural gradient的无偏估计。

\[\begin{aligned} \hat{\nabla}_{\lambda} L_{i} &= E_{q}[\eta_{g}(x_i,z_i,\alpha)] - \lambda \\ &= E_q[\alpha + N(t(x_{i},z_{i}),1)] - \lambda \\ &= \alpha + NE_q[(t(x_{i},z_{i}),1)] - \lambda \end{aligned}\]

最终有如下更新

\[\lambda_{t}=\lambda_{t-1}+\rho_{t}\hat{\nabla}_{\lambda} L^{t}_{i}\]

图四：随机变分推断算法

图四中可以看到，参数$\lambda$的更新不必等待局部参数$\phi$全部更新，仅使用单个样本的信息即可完成更新，因此降低了计算的开销。上述策略也很容易拓展到minibatch的情形。

小结

个人认为，随机变分推断最重要的一点是对natrual gradient的无偏估计。如果不能实现这一点，natural gradient的计算依赖于全部样本数据，算法依旧不能应用到大规模数据场景。

变分自编码(auto-encoding variation bayes)

个人认为变分自编码⁴最重要的一点是使用reparameterization trick改善了一些期望的估计，同时借助深度学习的策略放松了变分推断、随机变分推断只能处理特定的概率分布族的限制。

变分自编码器考虑如下问题，给定观测值$x$，我们希望得到一个编码器$q_{\phi}(z \vert x)$来得到隐变量，之后设计一个解码器$p_{\theta}(x \vert z)$将原数据从隐变量$z$中恢复出来。变分自编码器最终的优化目标为

\[L(\theta,\phi;x) = -D_{KL}(q_{\phi}(z \vert x) \vert \vert p_{\theta}(z)) + E_{q_{\phi}(z \vert x)}[\log p_{\theta}(x \vert z)]\]

在计算上述损失函数的梯度时，关于$\phi$的梯度通常使用如下策略估计

\[\nabla E_{q}[f(z)] = E_{q}[f(z)\nabla_{q}\log q_{\phi}(z)] \sim \frac{1}{L} \sum_{i=1}^{L} f(z)\nabla_{q}\log q_{\phi}(z_{l})\]

上述估计直接基于概率密度$q_{\phi}(z \vert x)$存在很大的方差。

重参数化提供了一种解决思路，对$z\sim q_{\phi}(z \vert x)$, 假设存在变换使得$z = g_{\phi}(\epsilon,x), \;\; \epsilon \sim p(\epsilon)$，则有

\[E_{q(z)} [f(z)] = E_{p(\epsilon)}[f(g_{\phi}(\epsilon,x))]\sim \frac{1}{L} \sum_{i=1}^{L} f(g_{\phi}(\epsilon_{i},x))\]

由此，可以得到$L(\theta,\phi;x)$的一个估计

\[\begin{aligned} \widetilde{L}(\theta,\phi,x) &= \frac{1}{L}\sum_{l=1}^{L}[\log p_{\theta}(x,z_{l}) - \log q_{\phi}(z_{l} \vert x)] \\ z_{l} & = g_{\phi}(\epsilon_{l},x), \;\; \epsilon\sim p(\epsilon) \end{aligned}\]

图五：变分自编码算法

可以看到，随机变分推断需要巧妙地设计global,local的关系以及先验概率，才能在优化目标中对global的部分进行无偏估计实现mini-batch。而在变分贝叶斯中，通过神经网络去拟合$z=g(\epsilon,x)$，我们可以通过对$\epsilon$的抽样来实现对目标的估计，从而轻易的视线mini-batch形式的计算并且极大的放松了先验分布的形式限制。

参考文献

[1] Argelaguet, Ricard, et al. “MOFA+: a statistical framework for comprehensive integration of multi-modal single-cell data.” Genome biology 21.1 (2020): 1-17.

[2] https://stats.stackexchange.com/questions/111759/exponential-family-observed-vs-expected-sufficient-statistics

[3] Hoffman, Matthew D., et al. “Stochastic variational inference.” Journal of Machine Learning Research (2013).

[4] Kingma, Diederik P., and Max Welling. “Auto-encoding variational bayes.” arXiv preprint arXiv:1312.6114 (2013). –>