最近的分析工作做了很多单细胞数据整合的尝试,对数据整合分析这个步骤也算是有了一点经验。正好看到NBT上发表了Characterizing the impacts of dataset imbalance on single-cell data integration1这篇工作,认真读一下,参考一下别人的经验。论文的通讯作者是多伦多大学的王波教授,之前的博客也介绍过他们组scGPT。个人还是很欣赏这篇工作的,感觉单细胞领域做了这么多方法之后,这种认真评估分析工具的使用效果的文章的重要性会逐步增强。虽然可能看起来没有什么大的创新,但是如果能够给研究者提供一份详细可靠的技术参考,这种贡献绝不亚于提出一个像scGPT这样的全新方法。
概述
- 单细胞数据整合方法是单细胞分析中的一个重要手段,通过将不同批次、不同样本的scRNA-seq数据整合到相同的空间中进行分析,极大的拓展了分析的空间,有助于找到更多潜在的生物信号。
- 现有的单细胞数据整合方法在样本不平衡的情形下的表现并不可靠,而样本不平衡现象在发育、癌症的情形下很常见,因此需要研究样本不平衡下各种数据整合方法的效果,以及对下游分析流程的影响。
- 作者在多个数据集上对当下最常用的5种整合方法,在多种下游任务上进行了评估,并对样本不平衡情形下的数据整合提出了相应的建议。
扰动实验设计
作者通过降采样的方式来模拟样本不平衡的情形。之后在一个统一的分析流程(Iniquitate) 下对各种扰动进行分析,基本流程如图一所示。
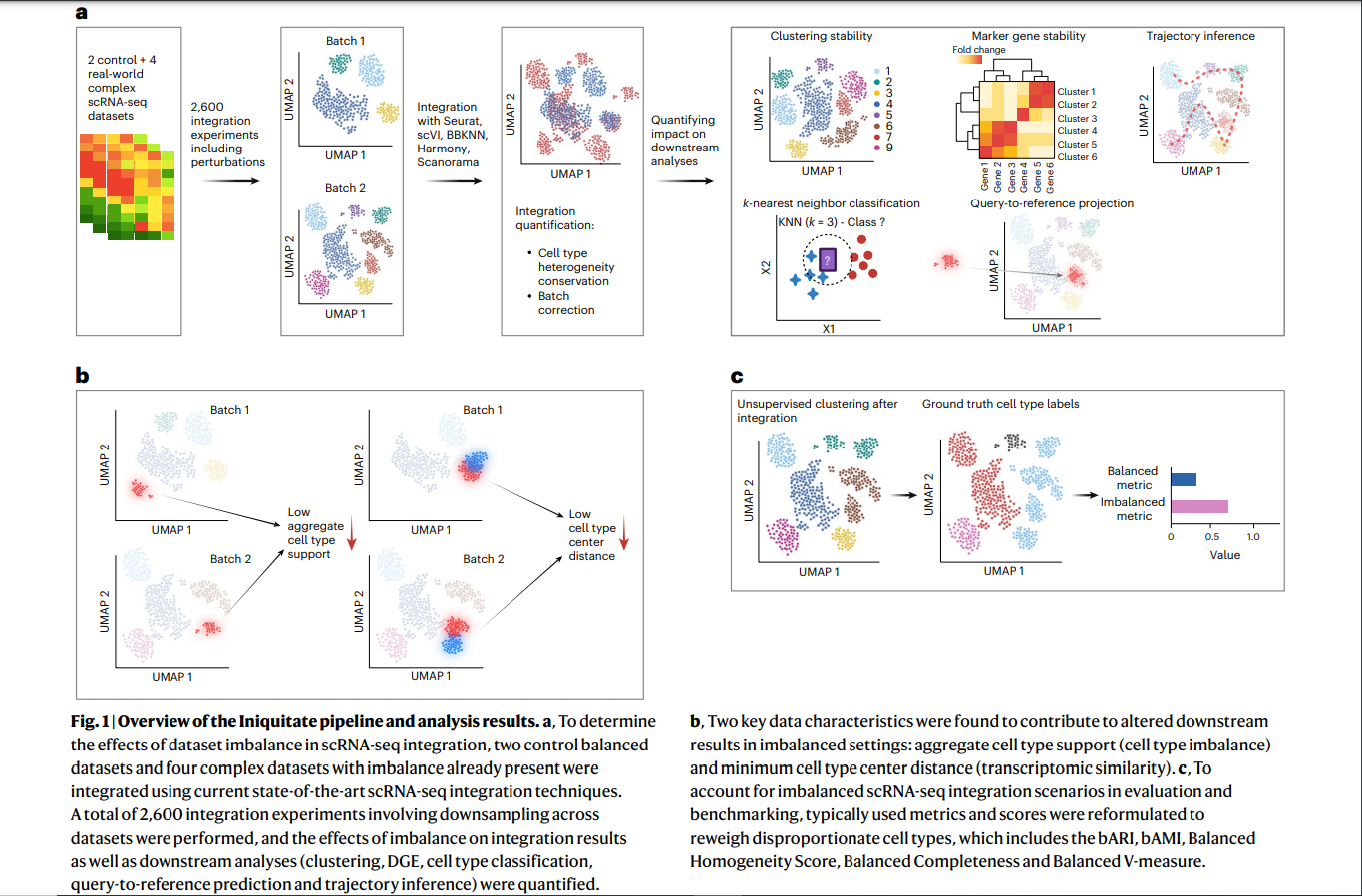
从图一可以看到,在完成数据扰动后,首先使用整合工具进行整合,整合效果主要有两个量化指标,cell type heterogeneity conservation 和 batch correction。
cell type heterogeneity使用$ARI_{celltype}$评估,期望整合后的聚类结果,能够清晰的区分celltype。batch correction使用$1- ARI_{batch}$评估,期望整合后各个batch能够混在一起,即在batch这个label上不能很好的聚类,因此使用1-ARI的指标。ARI的指标详见技术细节部分。
整合之后会在多个下游任务上分析样本不平衡带来的影响。具体内容见分析结果部分。
主要分析结果
样本不平衡导致细胞类型特异的整合效果
图二图三展示了PBMC上的实验结果,从a,b可以看到PBMC数据呈现两个清晰的batch,每个batch中包含6种相同的细胞类型。c中展示了两种扰动,对某种细胞类型降采样到10%或者直接去掉。
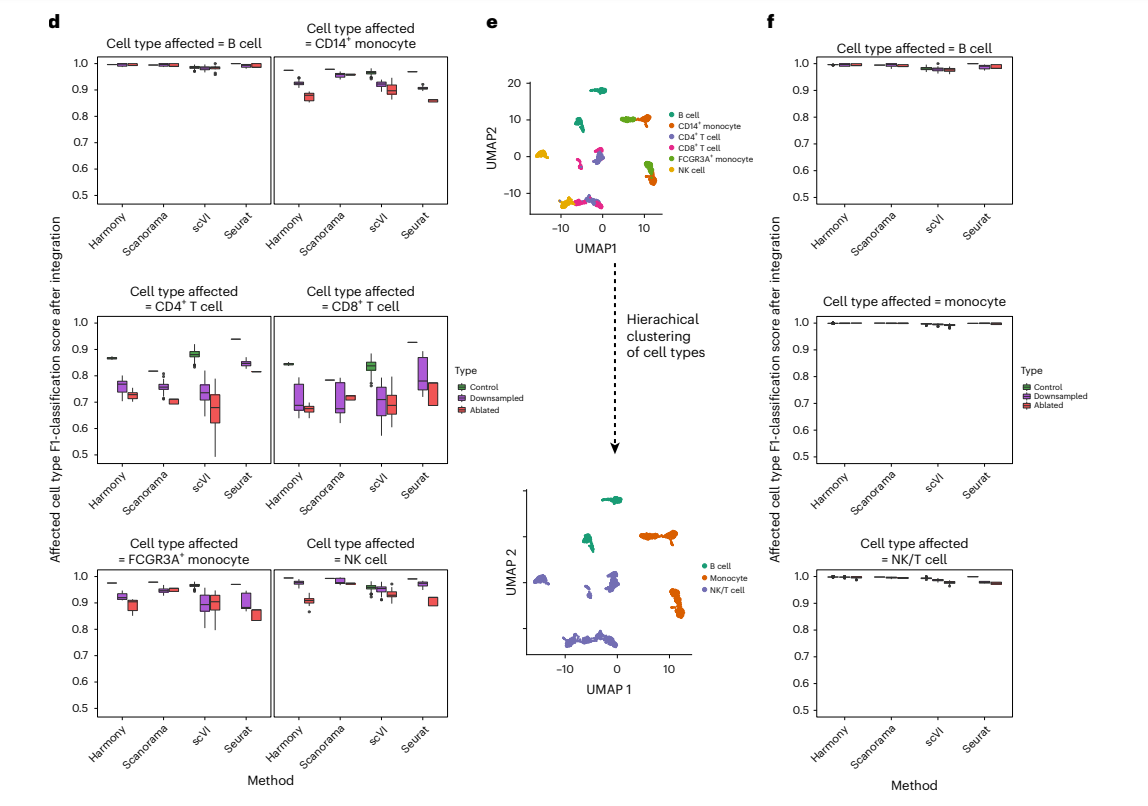
d中展示了,分别对不同细胞类型进行扰动,在不同的整合方法下KNN分类器的表现,可以清楚的看到扰动前后的分类效果变化是细胞类型特异的。B细胞几乎没有变化,剩下的5种细胞的变化很大,并且这种变化是各个整合方法中普遍存在的。这种变化是统计显著的。
作者猜测B细胞的这种稳定性是由于其转录组数据显著区别于其他五种细胞,进一步,作者将6种细胞分成3种细胞大类,在这3大类下重复先前实验,发现此时KNN分类效果变化很小。验证了他们的猜想。
作者定义了“最小类中心距离”(minimum cell type center distance)和“聚合细胞类型基数”(aggregate cell type support)两个指标来解释这种细胞类型特异的影响。但是正文和补充材料中都没有很详细的去阐释这个结果,很奇怪…… 简单点说,最小类中心距离度量了数据集中差异最小的两个细胞类型之间的距离,可以预见,这个指标如果很小的话,那么整合中很可能混在一起,从而影响后续分析。而这个聚合细胞类型基数看起来就是指定细胞类型的细胞数目,看起来就是个样本不平衡的指标而已……
以上实验验证了,在样本不平衡的情况下,某些细胞类型的整合存在问题(KNN分类器无法有效抓取细胞类型特征)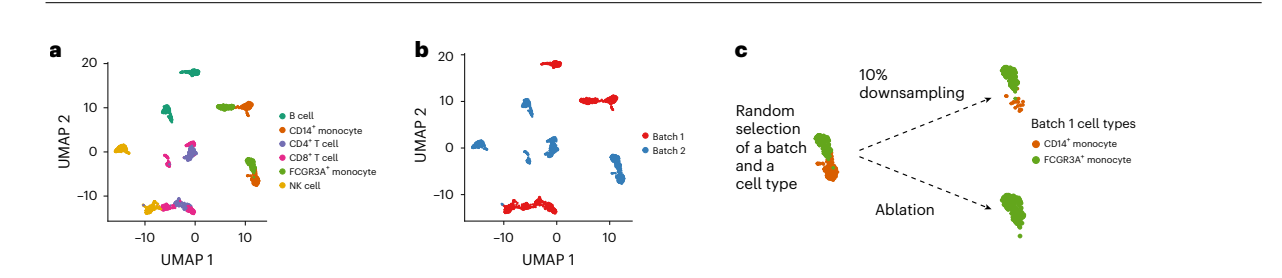
整合后聚类的稳定性
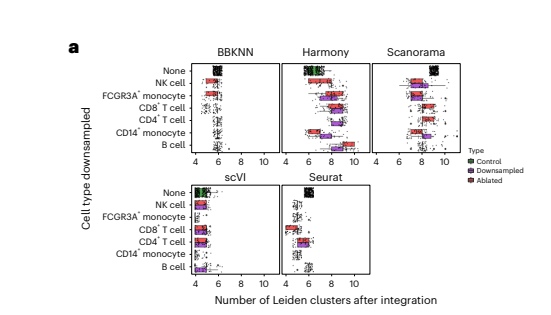
图四中展示了在PBMC数据上的扰动实验结果,作者从leiden聚类的cluster数目变化来考察这一点,几乎所有的方法都呈现出cluster数目的变化。为了保证结果的可靠性,作者对leiden聚类的resolution参数做了一定的限制,对每种方法选取method specific 的resolution 参数。具体流程如下:
- 遍历 0.1, 0.24, 0.5, 0.75, 1.0, 2.0, 3.0, 4.0, 5.0 这些resolution
- 在对照数据上进行整合,之后计算在给定resolution下,聚类数目与真实细胞类型数目的差异
- 记录与真实细胞类型数目差异最小的resolution。
- 对每一种整合方法,重复上述步骤50次,选择resolution的中位数作为后续扰动实验的最优resolution.
从结果中看,cluster数目的变化与整合方法和细胞类型都有关系,例如Harmony是所有方法中唯一呈现cluster数目增长的,而scVI仅在两个monocyte细胞类型上呈现数目的明显变化。总的来说,尽管在平衡的对照数据上,各种方法的聚类结果都有变化,但是扰动后的变化更加明显。
作者在这部分的结论是,样本不平衡会导致聚类数目的偏差,即使这种数目应当是稳定的,因为每次扰动后的细胞类型都是不变的,仅有比例的变化。Remark 1
对这个结论,还是有些质疑的。
- cluster数目是否是一个可靠的稳定性评估指标?在实际分析时,总会不停的尝试resolution来得到解释性更好的结果。所以cluster数目的变化并没人关注,只要能够找到一个resolution得到想要的结果就好了。比起评估相同resolution下cluster数目的变化,我觉得评估某个方法在多大的resolution范围下能够得到和真实的细胞类型数目一致的cluster数目可能更好些。这个范围一定程度上说明了结果的鲁棒性。
DGE和marker gene的稳定性
为了评估整合前后差异表达基因(DGE)的稳定性,作者定义了一个标记基因扰动分数来量化这种稳定性变化。具体细节如下:
marker gene perturbation score
- 对PBMC数据中,每个batch中的每个细胞类型,使用Wilcoxon rank-sum test确定其top 10 差异表达基因。之后将两个batch的top 10基因取并集,作为每个细胞类型对应的主要marker gene list。
- 之后进行数据整合,并应用leiden聚类划分cluster。
- 对每个cluster,计算其差异表达基因,之后对某个细胞类型的某个差异表达基因,计算其在所有cluster中的最高ranking。
- 在不同的扰动下,重复上述步骤N次,对每个marker gene,得到其对应的一组 max ranking。
- 定义marker gene perturbation score为该基因在多次扰动下的max ranking的标准差,即$\sigma(max\; marker\; gene \; ranking)$,显然,分数越低说明该marker gene的稳定性越好
- 进一步,可以定义某种细胞类型的marker gene 平均扰动分数,将其所有marker gene的得分取均值即可。
基于上述步骤,得到结果如下:
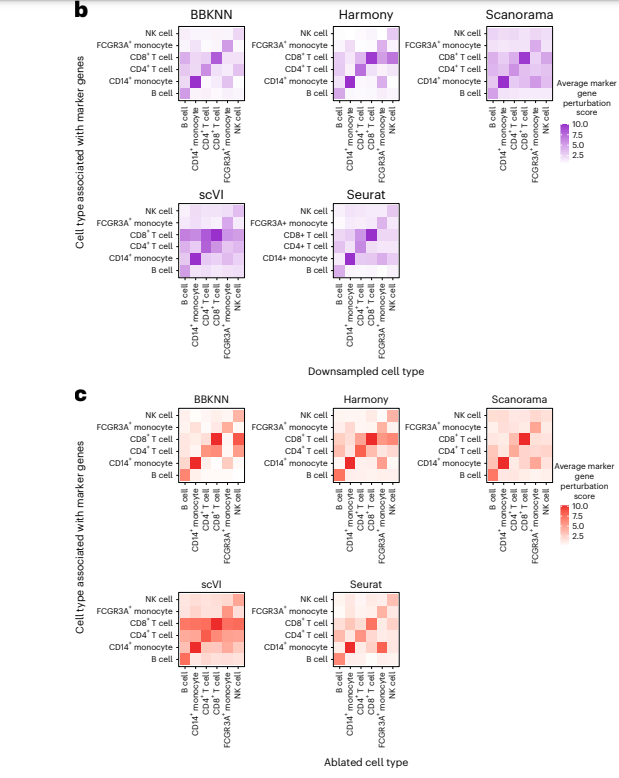
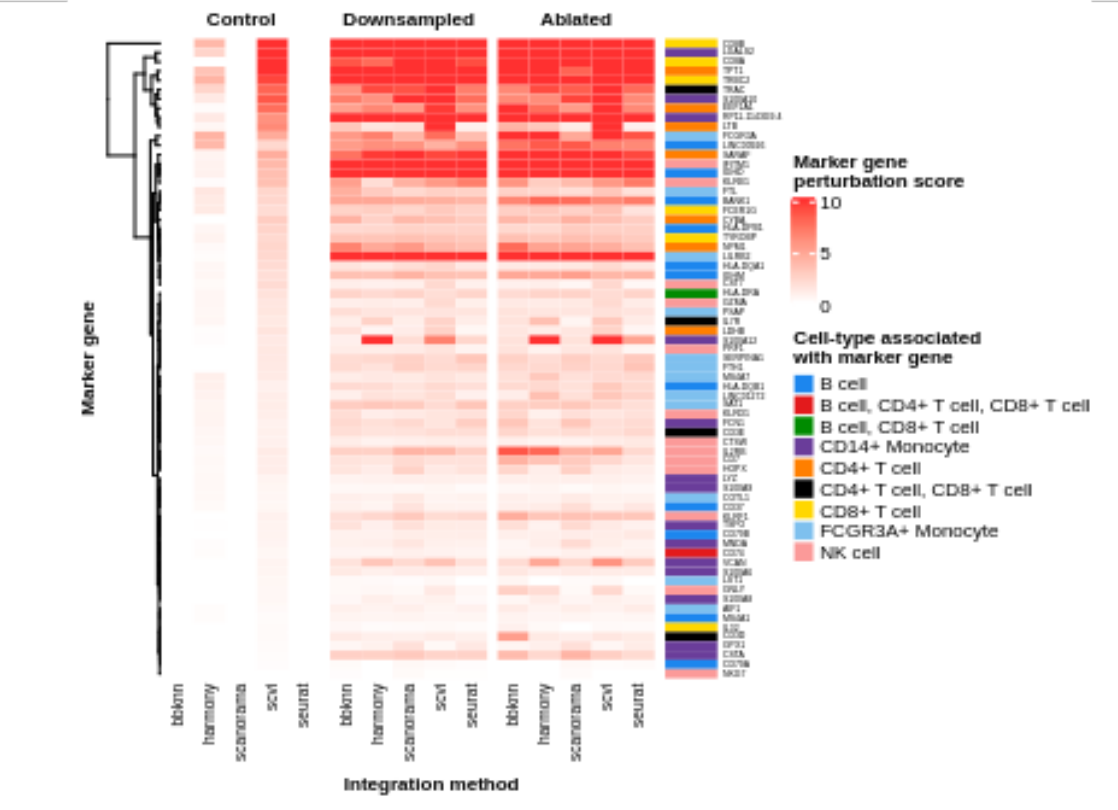
图六中展示了不同的细胞类型和整合方法下,扰动分数的变化情况。可以看到细胞类型、整合方法、以及不同扰动都会影响分数的变化。ANOVA 检验表明, 在特定marker gene, 整合方法和扰动细胞类型三个因素之间,扰动(样本不平衡)的影响是统计最显著的影响ranking的结果。图5中的结果表明,对哪种细胞类型进行扰动,哪种细胞类型对应的marker的rank 变化最显著(斜对角元素数值最大)。
这部分的结果说明,样本不平衡下的整合,会导致marker gene的显著变化。Remark 2:
个人对这部分结论存在质疑,因为样本不平衡本身就会导致marker gene的变化,这是统计检验方法本身的特征。研究应该关注的是,数据整合后,这种变化是否会加大。所以应当补充,在同一batch数据中,制造样本不平衡的情形,观察rank变化,并将其与整合数据的实验结果对比。
写到这里突然意识到一个问题,是不是这篇工作的所有结果,都需要在同一个batch下的样本不平衡下做一遍,然后再和整合后的样本不平衡结果对比?毕竟样本不平衡影响机器学习结果大家都知道......Query-to-reference projection and cell type annotation
基于ref数据注释query数据的细胞类型是单细胞数据分析中的常见情形,这种注释通常需要将两组数据整合到同一个空间中进行,作者用一个多模态PBMC数据做ref,然后将两个batch的数据分别与其整合并预测,得到结果如下:

在这里,作者提到仅对参考数据集做扰动。所有的实验都是按照Seurat v4的整合注释流程实现。因此结果的变化应当是Seurat v4的整合方法和扰动带来的。从结果看,在两个粒度下的注释,扰动T细胞后,几乎所有的细胞类型都无法有效注释。而扰动其他细胞基本都能有效注释。作者对这一现象的解释是T细胞的异质性。
这一小节的结果从细胞注释的层面说明,数据集中的样本不平衡会通过影响数据整合进一步影响细胞注释的结果。因此整合自动注释后,仍旧需要人工的marker gene校验。轨迹推断
主要结果如下:
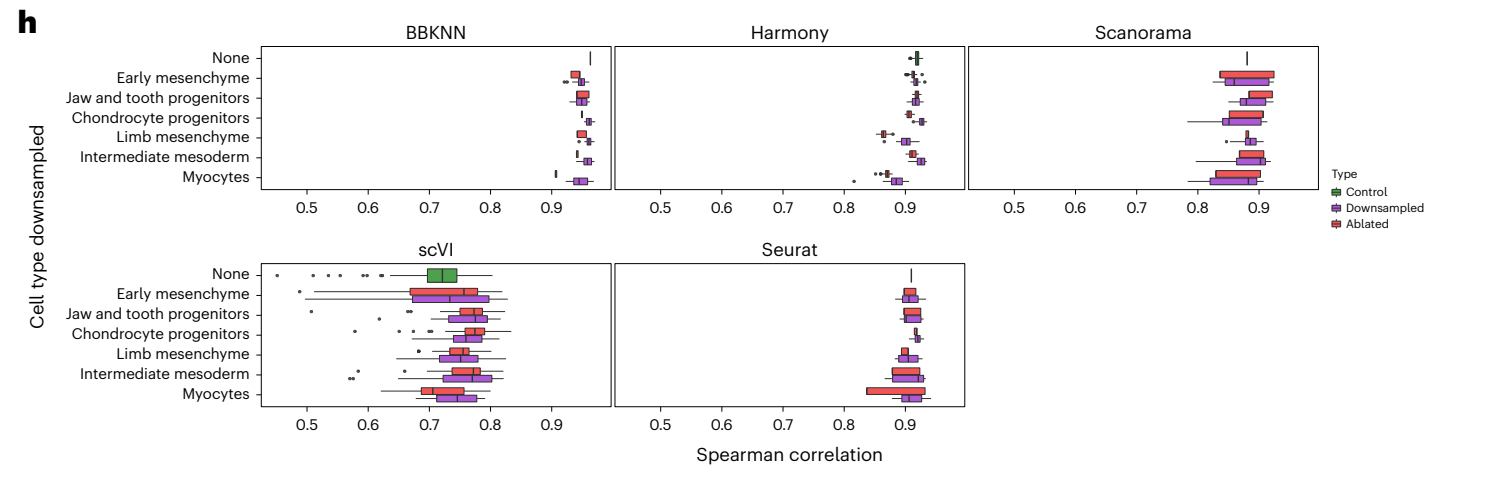
作者扰动哺乳动物发育数据集中的一个细胞Line中的不同细胞类型比例,统计整合前后轨迹推断的相关性。
这一小节的结果表明,样本不平衡下的整合,会显著影响轨迹推断的结果。Tumor compartment-specific effects of dataset imbalance
略
Balanced clustering metrics for imbalanced integration
这一节的结果没看出啥有意义的来,banlanced clustering metrics感觉实际分析也用不太到,做方法的时候倒是可以用,定义一个对自己方法有效的指标……
不平衡情形下的数据整合
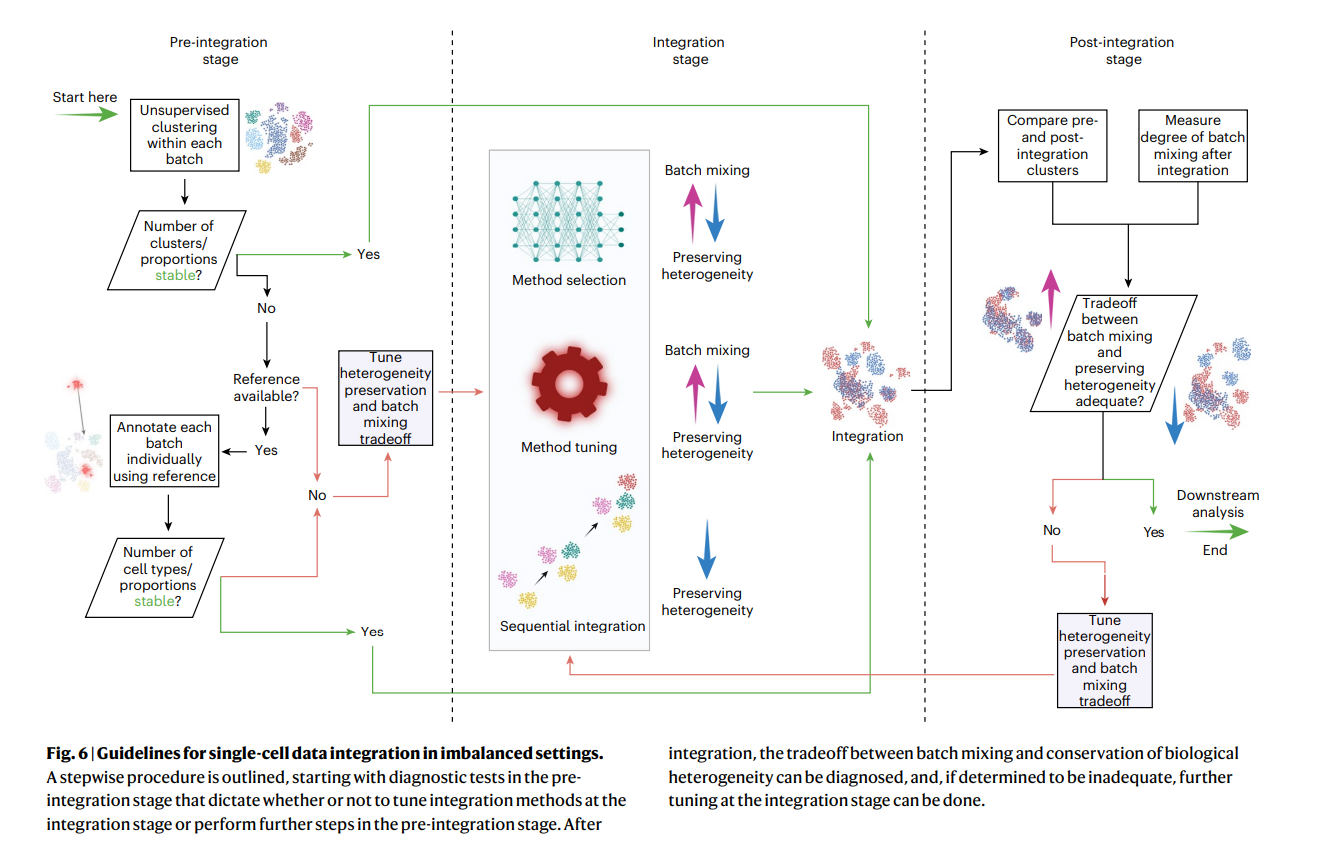
感觉并没有什么建设性的意见。还是要先验知识,还是要自行评估保留样本异质性和不同批次的混合程度的tradeoff ……有没有什么靠谱的工作能对这一点给出些指导啊?别全靠感觉了啊……好奇这方面的工作怎么做的,感觉应该有完善的空间。
技术细节
这里总结一下文章中使用的评估指标和统计检验策略。
ARI
对于聚类方法的评估,一个评价指标是Rand Index。考虑如下情形:
给定一个样本集合$S = {s_{1},…,s_{n} }$以及两个划分$X,Y$. 考虑如下列联表:
| X\Y | $Y_{1}$ | $Y_{2}$ | … | $Y_{s}$ | Sums |
|---|---|---|---|---|---|
| $X_{1}$ | $n_{11}$ | $n_{12}$ | … | $n_{1s}$ | $a_{1}$ |
| $X_{2}$ | $n_{21}$ | $n_{22}$ | … | $n_{2s}$ | $a_{2}$ |
| … | … | … | … | … | … |
| $X_{r}$ | $n_{r1}$ | $n_{r2}$ | … | $n_{rs}$ | $a_{r}$ |
| Sums | $b_{1}$ | $b_{2}$ | … | $b_{s}$ | n |
其中$n_{ij}$为划分$X_{i}$与$Y_{j}$的交集数目。定义
- \[\begin{equation} a: \# \{(s_{i},s_{j}) \vert s_{i},s_{j} \in X_{k}, Y_{l}, \; \forall k,l\} \end{equation}\]
- \[\begin{equation} b: \# \{(s_{i},s_{j}) \vert s_{i}\in X_{k^{'}},Y_{l^{'}},s_{j} \in X_{k}, Y_{l}, \; \forall k,l,k^{'},l^{'}\} \end{equation}\]
- \[\begin{equation} c: \# \{(s_{i},s_{j}) \vert s_{i}\in X_{k^{'}},Y_{l},s_{j} \in X_{k}, Y_{l}, \;\forall k,k^{'},l\} \end{equation}\]
- \[\begin{equation} d: \# \{(s_{i},s_{j}) \vert s_{i}\in X_{k},Y_{l^{'}},s_{j} \in X_{k}, Y_{l}, \;\forall k,l,l^{'}\} \end{equation}\]
- a 表示两个样本在划分X,Y中都分别属于同一个cluster的样本pair数目, b 表示两个样本在划分X,Y中都分别属于不同的两个cluster的样本pair数目,c 表示两个样本在划分Y中属于相同的cluster,在划分X中属于两个不同的cluster的样本pair数目, d 表示两个样本在划分X中属于相同的cluster,在划分Y中属于两个不同的cluster的样本pair数目。
- a,b 表示两个划分中一致的样本pair, c,d 表示两个划分中不一致的样本pair
a,b,c,d可以通过上面的列联表进行表示。
- $a = \sum_{ij}\tbinom{n_{ij}}{2}$, 因为满足两个样本在X,Y中都分别属于同一个集合$X_{i},Y_{j}$, 对每个这样的$X_{i},Y_{j}$分别考虑,$X_{i} \cap Y_{j}$中的任意两个元素都符合定义,有$\tbinom{n_{ij}}{2}$对满足条件的样本pair。
-
注意到 a,d 对应的集合的并集为 两个样本在划分X中属于统一个cluster的样本pair $={(s_{i},s_{j})\vert s_{i},s_{j} \in X_{k} }$。因此有
\[\begin{equation} \begin{aligned} a+d &= \sum_{k} \tbinom{a_{k}}{2} \\ d &= \sum_{k} \tbinom{a_{k}}{2} - a = \frac{1}{2}(\sum_{k}a_{k}^2 - \sum_{ij}n_{ij}^{2}) \end{aligned} \end{equation}\] - 类似的有$c=\sum_{l} \tbinom{b_{l}}{2} - a = \frac{1}{2}(\sum_{k}b_{l}^2 - \sum_{ij}n_{ij}^{2})$
- $b= n-a-c-d$
Rand index 定义如下:
\[RI = \frac{a+b}{a+b+c+d} = \frac{a+b}{\tbinom{n}{2}}\]显然,$RI\in[0,1]$,$RI$度量了两个划分的一致性。$RI$存在的一个问题是对于完全随机的两个划分,RI的结果不一定为0,可以证明,在完全随机划分(permutation model)的情形下,有 \(\begin{equation} \begin{aligned} \mathbb{E}_{\text{perm}}[\text{RI}(\mathcal{X}, \mathcal{Y})] &= \frac{2Q^X_1 Q^Y_1 - {N \choose 2}(Q^X_1 + Q^Y_1) + {N \choose 2}^2}{\tbinom{N}{2}} \\ Q^X_1 &= \sum_{k} {a_{k} \choose 2} \end{aligned} \end{equation}\)
\[\begin{equation} \begin{aligned} ARI &= \frac{RI - \mathbb{E}_{\text{perm}}[\text{RI}]}{\max{RI} - \mathbb{E}_{\text{perm}}[\text{RI}] }\\ &= \frac{\binom{N}{2}\sum_{k,m}\binom{n_{km}}{2}-\sum_{k}\binom{a_k}{2}\sum_{m}\binom{b_m}{2}}{\frac{1}{2}{\binom{N}{2}}[\sum_{k}\binom{a_k}{2}+\sum_{m}\binom{b_m}{2}]-\sum_{k}\binom{a_k}{2}\sum_{m}\binom{b_m}{2}} \end{aligned} \end{equation}\]在上述校正后,ARI为两定义的度量, 并且在随机情形下度量为0。
ANOVA
To do.
总结
作者对单细胞分析中数据整合过程中的类别不平衡进行了分析,验证了类别不平衡会显著的影响下游的分析。但是感觉有的分析存在逻辑漏洞,以及从结果上看数据整合还是一个相对主观的步骤,非常依赖于分析者的生物学先验和对数据集之间差异的估计。但不管怎样,文章揭示了现有方法和分析流程的一个漏洞,这个新的方法和流程提供了改进空间,是很有意义的工作。
参考文献
- [1] Maan, H., Zhang, L., Yu, C. et al. Characterizing the impacts of dataset imbalance on single-cell data integration. Nat Biotechnol (2024). https://doi.org/10.1038/s41587-023-02097-9
- [2] Alexander J Gates and Yong-Yeol Ahn (2017). “The Impact of Random Models on Clustering Similarity” (PDF). Journal of Machine Learning Research. 18: 1–28.
- [3] https://en.wikipedia.org/wiki/Rand_index#Adjusted_Rand_index